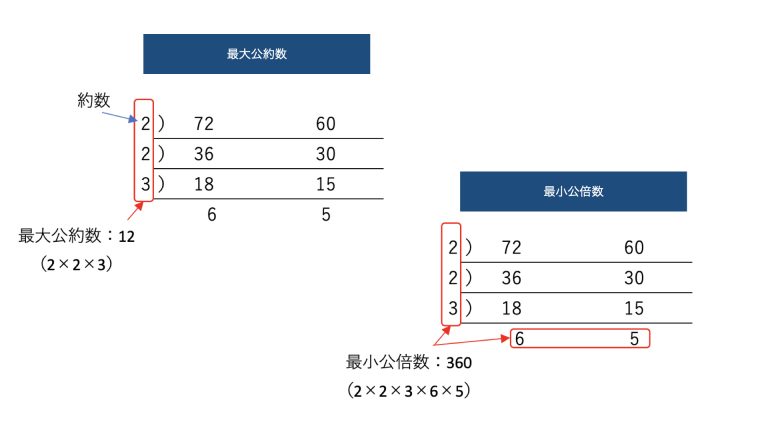
最大公約数 はここで終わり でしたが、最小公倍数の場合は 割り算を続けます。 ルール1 2つ以上で共通で割れたら割って商を下に書く。 ルール2 割れなかった数は、 そのまま下に書く。 2 と 12 は共通の 2 で割れますので、商 1, 6 を書きます。 しかし、7 は 2 では割れませんので、そのまま 7 を下に書きます。 そして、 左側と下の数をかけ算 します。 2 3 2 1 7 6 = 504 よって、 12, 数の性質に関する問題の一覧 倍数と約数の問題 わり算のあまりと等差数列 最大公約数と最小公倍数 素因数分解の問題 既約分数の個数 四捨五入とその範囲 分数と小数の応用 n進法に関する最大公約数 ⇒ 公約数の中でも最大のもの 最大公約数の意味は、下記が参考になります。 最大公約数とは?1分でわかる意味、求め方、問題、16と40の値、最小公倍数との関係 まとめ 今回は公約数について説明しました。意味が理解頂けたと思います。

整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん
公約数 公倍数 問題
公約数 公倍数 問題- 「公倍数」「公約数」について。 「最大公約数」「最小公倍数」について。 実践問題を解いてみよう! 問1:108と360の最大公約数と最大公倍数を求めなさい。 手順①:2つの数をそれぞれ素因数分解する。 手順②:最大公約数を求める。 整数の性質 (公倍数・公約数) 21年7月7日 最小公倍数・約数・最大公約数のプリントです。 公倍数や公約数の求め方は、この学習の後に学習をする異なる分母の通分や約分の学習の際に使われます。 何度も練習をして、数字を見ただけで最小公倍数や最大



3
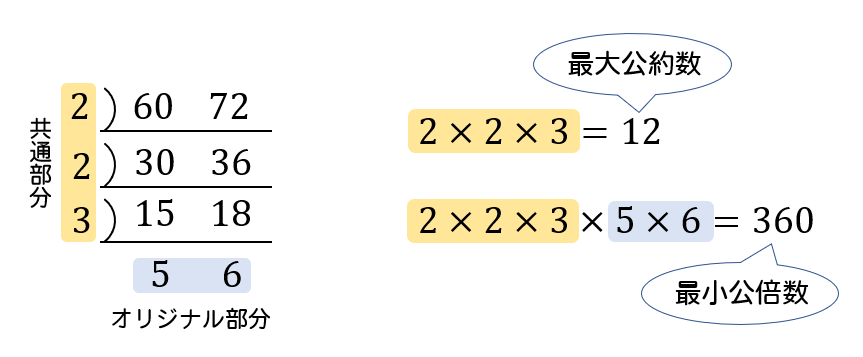
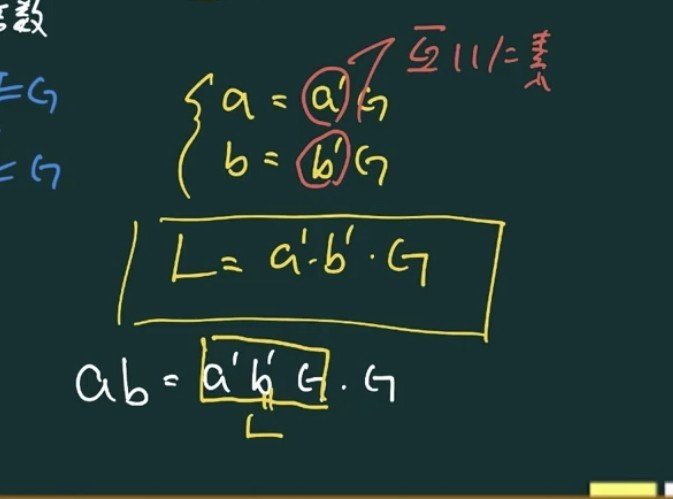
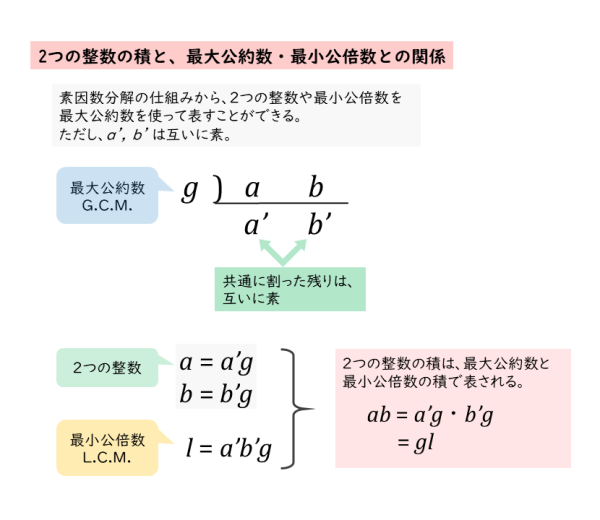
最大公約数と最小公倍数 すごい! 宿題めっちゃ楽! 塾の宿題の時に役立つ! 分数の約分に役に立ちました。 ちなみにアスペクト比って約分してもいいんですか? さて、ここまで公約数と公倍数についてみてきましたが、実はこの2つには大きな関係があります。 それは A = G a , B = G b で( a, b は互いに素、 G は最大公約数) A, B の最小公倍数が L であるとき L = G a b である。 という関係です。 すなわち最小公倍数は最大公約数を使ってかけるということです。 具体的にやってみると一番わかりやすいです。 例えば先ほどの12と18だと 12 = 6 数が3個以上の場合は? 本題はこっち。 まず調べる数が不定なので、引数を配列に変更してみます。 次にアルゴリズム部分ですが、数が増えたとは言っても 変数a,b,cについて 『aとbとcの最大公約数』 = 『aとbの最大公約数』と『c』 の最大公約数 『aと
・全体を等しく分ける場合は、最大公約数を使う。 ブロックを積み上げて、等しい立体を作るので、最小公倍数を使う。 cm、30cm、12cmの最小公倍数は、60。 1辺が1m以上なので、必要な長さは、60×2=1cm。 縦のブロックの数は、1÷=6 ここでは、最大公約数と最小公倍数の積に関する性質を見ていきます。互いに素な2つの自然数の最小公倍数互いに素な2つの自然数を考えてみます。例えば、 $5,9$ について考えてみましょう。最大公約数は $1$ で、最小公倍数 ※子ども達が"公倍数"と出会う授業の板書データがなかったです。申し訳ありません。 3時間目公倍数を使って 授業日:19年9月5日 執筆日:年3月14日 4時間目約数と公約数について 授業日:19年9月6日 執筆日:年3月14日
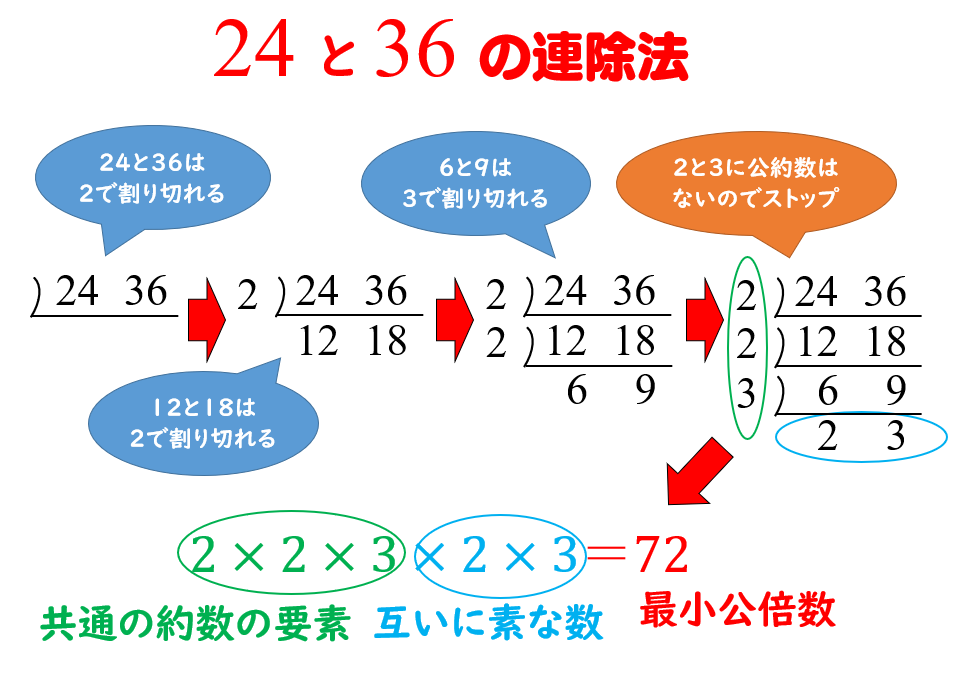
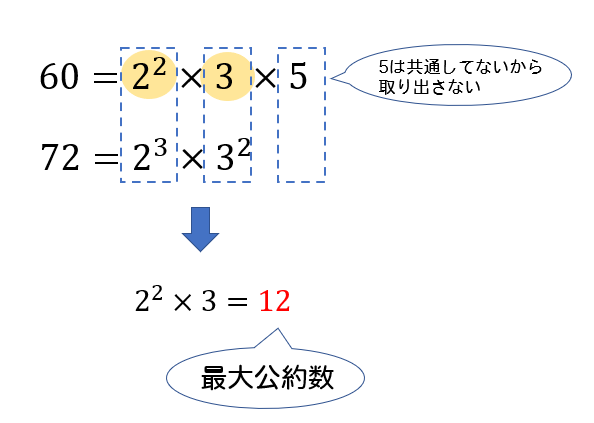
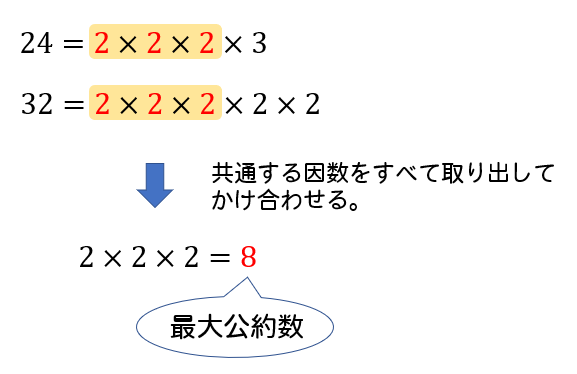
・ 12,−18 12, − 18 の最小公倍数は 36 36 ・ 3,5 3, 5 の公約数は −1,1 − 1, 1 ,最大公約数は 1 1 .したがって, 3 3 と 5 5 は互いに素. 注意 ・約数や公約数といったときに正の数のみを対象とする流儀もあります. ・公約数や公倍数は一般には複数ありえますが,最大公約数や最小公倍数はただひとつに決まります. ・最大公約数,最小公倍数は必ず 正の数 です. 倍数関係の基本性公約数・最大公約数の簡単な見つけ方|連除法を使う方法と使わない方法 約数 を習ったら次は"公約数"や"最大公約数"を習うと思います。 ただ、約数が漏れなく見つけることができるようになれば、公約数や最大公約数を求める問題はスムーズに素因数分解を活用して、これらの最大公約数、最小公倍数を求めてみましょう。 (1)\(60, \ 72\) をそれぞれ素因数分解をします。 最大公約数とは、それぞれの共通する素因数をすべて取り出して掛け合




最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場



公約数と公倍数 わかる数学
公倍数を計算したい2つの数といくつまで表示するかを入力し「公倍数を計算」ボタンをクリックすると、入力された値の公倍数を小さい方から指定された数まで表示されます。 (1~) 小さい方から 個まで (1~100) 12と15の公倍数を、小さい方から10個まで求める 12と15の公倍数:60, 1, 180, 240, 300, 360, 4, 480, 540, 600 約数・倍数の計算 ・ 素因数分解 ・ 最大公約数 (2つの数) 公約数は最大公約数の約数となる 先程の例で考えてみましょう。 16と40の公約数は 1、2、4、8 16と40最大公約数は 8 8の約数は 1、2、4、8 となるので、 公約数は最大公約数の約数となります。 最大公約数と最小公倍数の積は元の数の積と同じ 約数と倍数② 公約数と公倍数とは 「公」という字は、「みんなの」とか「共通の」という意味です。 「公約数」の意味は、2つ以上の数の「共通の」約数ということ。 2つの数のファミリーの両方にいるメンバー(約数)ということですね。 では「12」ファミリーと「18」ファミリーの約数たちから公約数を探してみましょう。 12の約数は、 1, 2, 3, 4, 6, 12 でした。 18の約数も小さ



公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun




Lcm最小公倍数 Gcf最大公約数の英語表現を覚えよう ゆう アメリカ生活終了 英語勉強
2つの数の公約数を計算します。 公約数を計算したい2つの数を入力し「公約数を計算」ボタンをクリックすると、入力された値のすべての公約数と公約数の数が表示されます。 (1~) 36と48の公約数を求める 1, 2, 3, 4, 6, 12 公約数の数:6 約数・倍数の計算 ・ 素因数分解 ・ 最大公約数 (2つの数) ・ 最大公約数 (3つの数) ・ 約数 ・ 公約数 (2つの数) ・ 公約数 (3つの数) ・ 最小公倍数 公倍数と公約数 問題 次の問いに答えなさい。 ① 26と60の公倍数を小さい順に3個求めなさい。 ② 36と54の公約数を全て求めなさい。 ③ 12と18と48の最小公倍数と最大公約数を求めなさい。 問1 解き方 ある整数を1倍・2倍・3倍・・・のように整数を倍にし 素因数分解によって「 約数の個数と総和 」が求められる事、そしてそこから見える「 約数と公約数のしくみ 」、「 ユークリッドの互除法 」という最大公約数の求め方。 そして「 倍数と公倍数のしくみ 」と素因数分解との関係性、「 最大公約数と最小



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




公約数と公倍数の自主学習ノート例 家庭学習レシピ
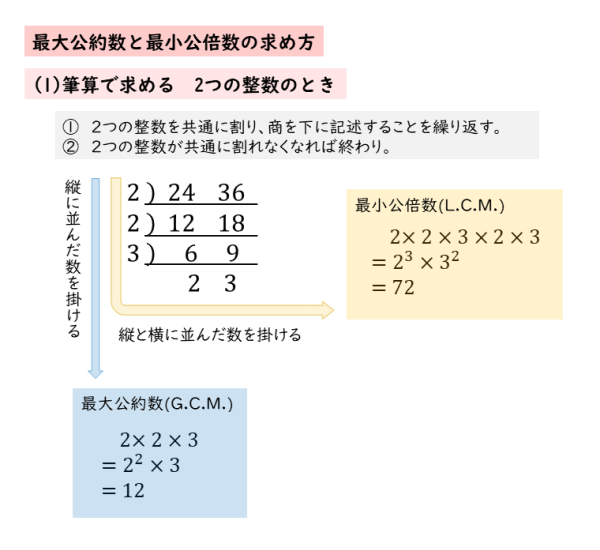
算数の公約数とは まずは公約数の意味や公倍数との違いから見ていきましょう。 そもそも約数とは 約数とはある数をやり切ることができる整数(主に自然数)を指しますが、これは その数を掛け算で表した時に登場する数 のことです。 例えば、18を自然数同士の掛け算で表すと以下の3 最小公倍数の求め方 例)16と30の最小公倍数を求める。 ① 下記のように数字を並べて、公約数で割っていく。 ② 公約数が1になるまで①を続ける。 ③ 最後に左の数字と、下の数字を全てかけたものが最小公倍数と言う。 最小公倍数は\(2\times3\times2\times5 = 60\)倍数・約数 2つの整数a,bがあって, a=b×q (qは整数) のとき,aはbの倍数,bはaの約数として定義されます。 小学校では,一度に両方の概念を与えると混同しやすいので,別々に扱います。 それで,倍数については,下の例のように,具体的な数をあげて



最大公約数 最小公倍数 Geogebra



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ
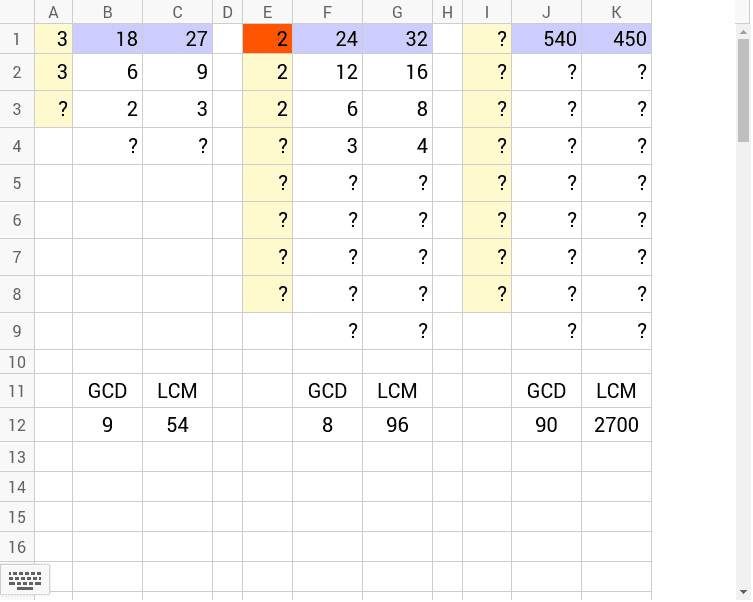
最大公約数と最小公倍数(数の問題) 最大公約数と最小公倍数 次の問いに答えなさい。 (1)2つの整数84とAがあります。 この2つの整数の最大公約数は14で。最小公倍数は4です。 このとき,整数Aはいくつですか。 (2)2つの整数A,Bがあります。次の にあてはまる数を答えなさい。 (1)48の約数は全部で 個あります。 (2)50以上の素数で2番目に小さい数は です。 (3)255、459、1122の最大公約数は です。 (4)36、60、84の最小公倍数は です。 (5)2けたの整数で、6の倍数で144の約数でもあるのは 個あります。最大公約数・最小公倍数を求める 最大公約数と最小公倍数を計算します。 けれど、手で計算するのも練習です。 検算などに使ってください。 公倍数・公約数を見つける2以上(1千万)以下の整数を2個以上入力してください。 数字以外の入力は




整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん



最小公倍数 最大公約数の求め方はこれでいいんですか 素因数分解は Yahoo 知恵袋
最大公約数とは、2つ以上の正の整数に共通な約数(公約数)のうち最大のものを言う。 最小公倍数とは 最小公倍数とは、2つ以上の正の整数の共通な倍数(公倍数)のうち最小のものを言う。 作成するプログラムの仕様 処理概要 メイン処理 ①変数(a、b)に任意の整数をセット(今回は60と72)。 ②最大公約数算出関数 gcf ()を呼び出し、結果を出力する。 ③最小公倍数算出関数 の公倍数が, 最小公倍数が ということは (「任意の公倍数は最小公倍数の倍数」を利用した) より, は の公約数であることが示された. の最大性より, である. かつ から、 を代入して gcd (a,b)=gcd (b,a) が成り立つことを示す. とする. は の公約数なので「最大公約数は任意の公約数の倍数」であることより と表せる。 同様に, は の公約数なので「最大公約数は任意の公約数の倍数 また、公約数の中で、一番大きいものを最大公約数(greatest common divisor、略して、GCD とも書く) といいます。先ほどの例であれば、 $6$ と $8$ の公約数は $\pm1,\pm2$ で、最大公約数は $2$ となります。 倍数についても、「共通する倍数」を考えることができます。




倍数と約数 最大公約数を求める 練習問題 Youtube




C言語 最小公倍数の求め方 3つ以上も可 だえうホームページ




最大公約数 最小公倍数 中学受験 算数 さんすう



最大公約数とは 意味や簡単な求め方 計算問題 受験辞典




5年算数 整数の性質 公倍数 公約数の利用 長方形と正方形 マドリト フリーランスデザイナーのブログ




最大公約数と最小公倍数の応用 無料で使える学習ドリル
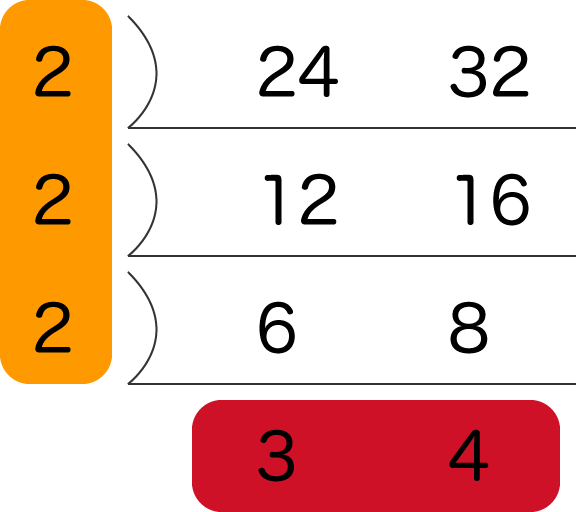



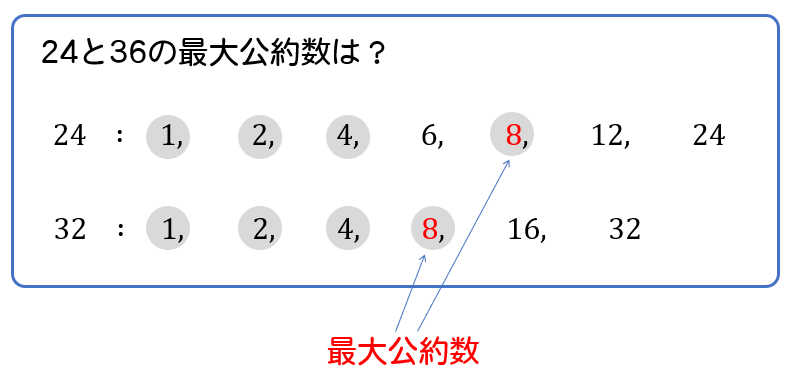
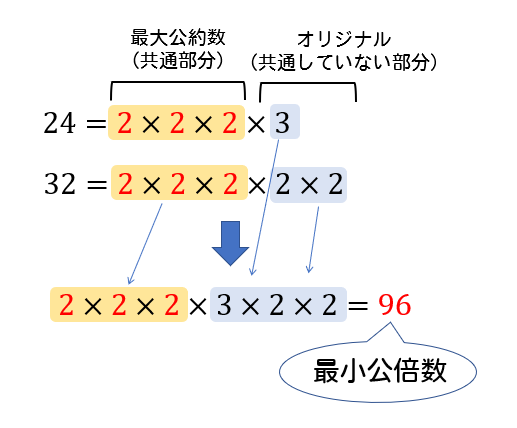
24と32の最大公約数と最小公倍数 Irohabook




中学受験 3つの数の最小公倍数 最大公約数の求め方 特殊なパターンも図解 そうちゃ式 受験算数 新1号館 数論 特殊算




オンライン学習会 今日は最大公約数です たぶお Sapix サピックス A1 養成講座
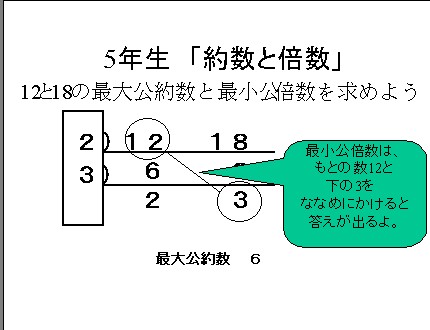



算数4年から6年



最小公倍数の求め方 大人のやり直し算数の第一歩 計算方法の解説 無料




Android向けの最大公約数 最小公倍数 Apkをダウンロードしましょう



最大公約数とは 意味や簡単な求め方 計算問題 受験辞典



最大公約数と最小公倍数 計算機 Androidアプリ Applion




5年算数 整数の性質 公倍数 公約数 の簡単な求め方 マドリト フリーランスデザイナーのブログ



最大公約数とは 意味や簡単な求め方 計算問題 受験辞典




小学5年生 算数 8月 約数と公約数 公倍数 公約数の利用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



最大公約数の求め方 大人のやり直し算数の第一歩 計算方法の解説 無料




公約数 公倍数の求め方 Z Square Z会




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学




2講 最大公約数 最小公倍数 1節 約数と倍数 問題集 3章 整数の性質



3




数の性質 実践問題 最大公約数と最小公倍数から2つの整数を求めるには
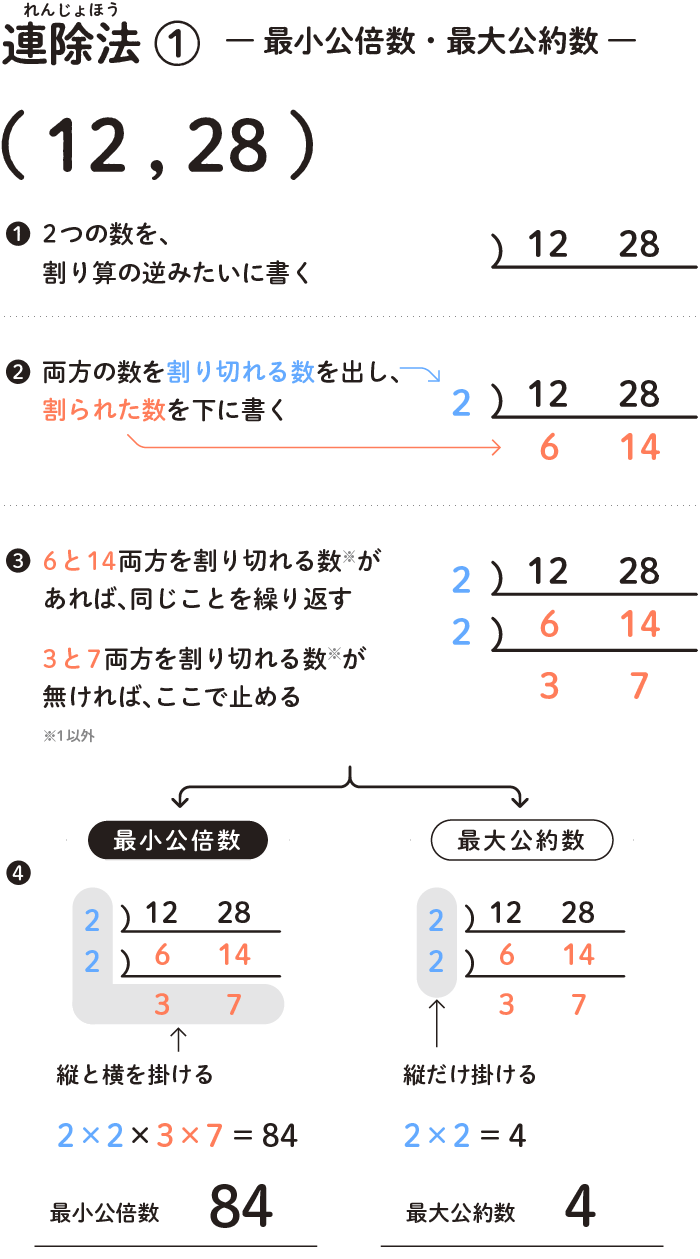



5年算数 整数の性質 最小公倍数 最大公約数 連除法を使う マドリト フリーランスデザイナーのブログ
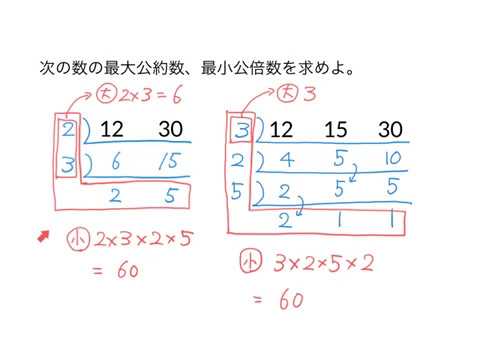



最大公約数と最小公倍数のはしご算 Youtube




最大公約数と最小公倍数の積の性質の2通りの証明 高校数学の美しい物語



最大公約数と最小公倍数




最小公倍数 最大公約数 小学5年生 計算無料プリント 小学生算数問題




公約数 最大公約数 公倍数 最小公倍数 求め方 ぐらたん塾



1



2



最大公約数と最小公倍数
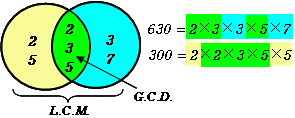



最大公約数と最小公倍数 高精度計算サイト




中学受験 素因数分解 すだれ算 連除法 はしご算 で最小公倍数 最大公約数を求める方法 そうちゃ式 受験算数 新1号館 数論 特殊算



最小公倍数 最大公約数のドリル
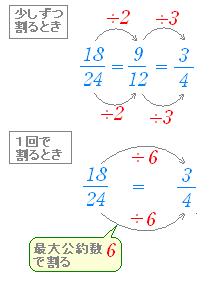



最大公約数 最小公倍数
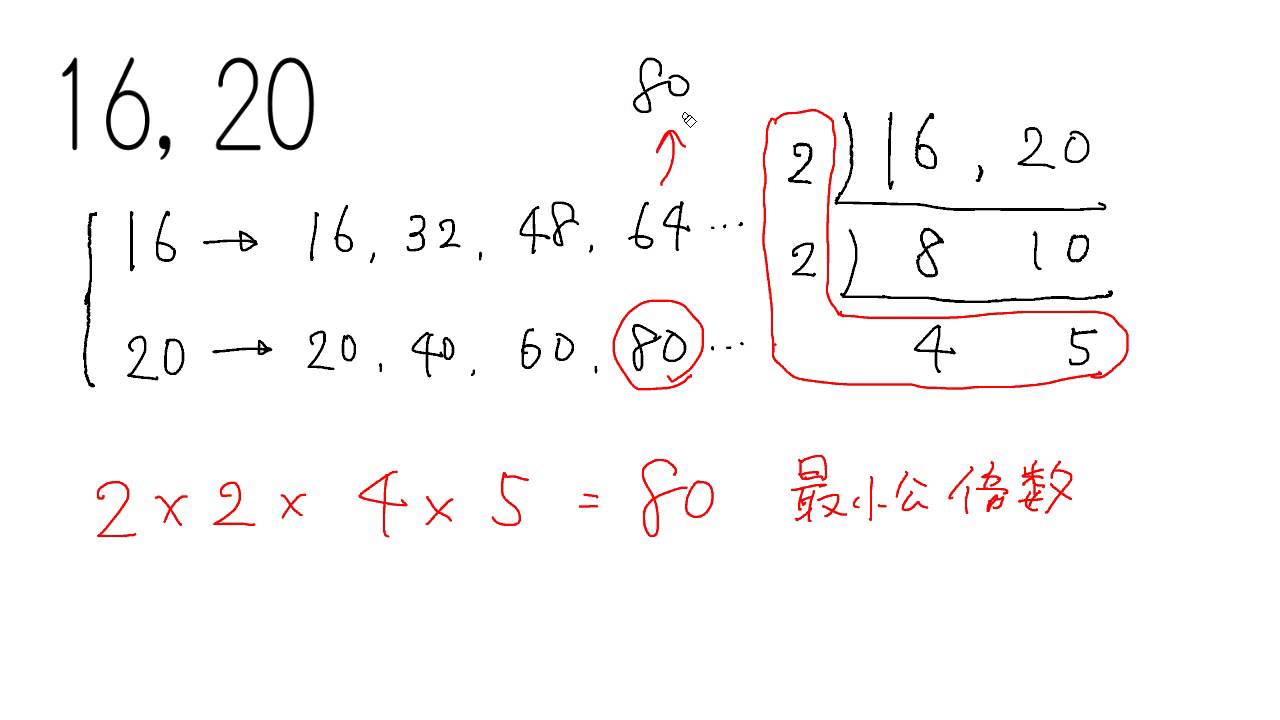



最大 公約 数 求め 方 約数と倍数の基本 最大公約数と最小公倍数の求め方まで小学生にわかる教え方 Yeah Math Stg Origin Aegpresents Com




高校数学 最大公約数と最小公倍数の求め方のコツ 数樂管理人のブログ




最大公約数と最小公倍数 つくば理数塾 Scimath




高1です 数学がわかりません 教えてください 最大公約数と最小公 その他 学校 勉強 教えて Goo




最小公倍数と最大公約数の式 倍数 約数シリーズ Youtube
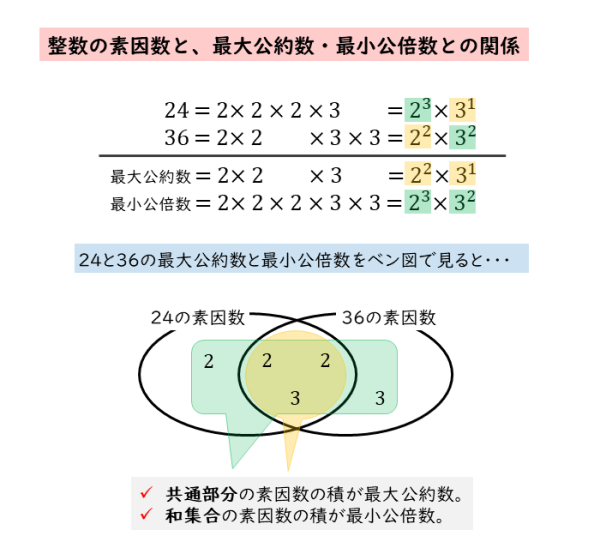



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




最小公倍数を求める練習問題 計算ドリル 問題集 数学fun




最大 公約 数 求め 方 約数と倍数の基本 最大公約数と最小公倍数の求め方まで小学生にわかる教え方 Yeah Math Stg Origin Aegpresents Com



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




高校数a 整数 最大公約数 最小公倍数から数を求める オンライン無料塾 ターンナップ Youtube



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




高校1年生の数学i 最大公約数 最小公倍数 について なぜこのような 数学 教えて Goo




数的推理 Ask公務員 公務員試験に合格するための情報サイト




5mx86 最小公倍数 最大公約数 分数のたし算 親子でどんぐり




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



ゼミネット公務員チャンネル 公務員試験対策講座 ここから確認 数的推理 再 入門



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




公約数 公倍数の求め方 Z Square Z会



5年算数 偶数奇数最大公約数最小公倍数 教え方



最大公約数と最小公倍数 オモワカ整数 4 全21回 数学専門塾met Note




最大公約数と最小公倍数の応用 無料で使える学習ドリル



数学i Aチェック リピート 第6章 3整数の性質 2 最大公約数 最小公倍数 Pukiwiki




最大公約数と最小公倍数の計算プリント Irohabook




幼稚園から中学受験まで 最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 養成講座



3



3



2



Java 最大公約数と最小公倍数を求める え のう



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん



最大公約数 最小公倍数 On The App Store



最大 公約 数 求め 方 約数と倍数の基本 最大公約数と最小公倍数の求め方まで小学生にわかる教え方 Yeah Math Stg Origin Aegpresents Com



覚えておきたい最小公倍数と最大公約数の求め方 盛り上がれ秋田
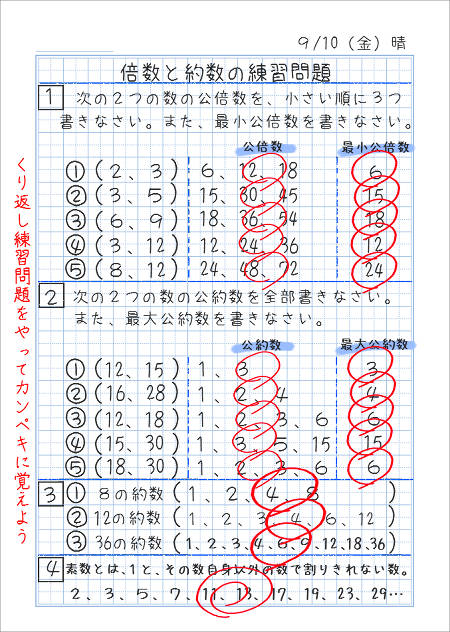



公約数と公倍数の自主学習ノート例 家庭学習レシピ



最大公約数の求め方 大人のやり直し算数の第一歩 計算方法の解説 無料




最大公約数 最小公倍数 L Ga B Gl Ab の原理 数学1a Youtube
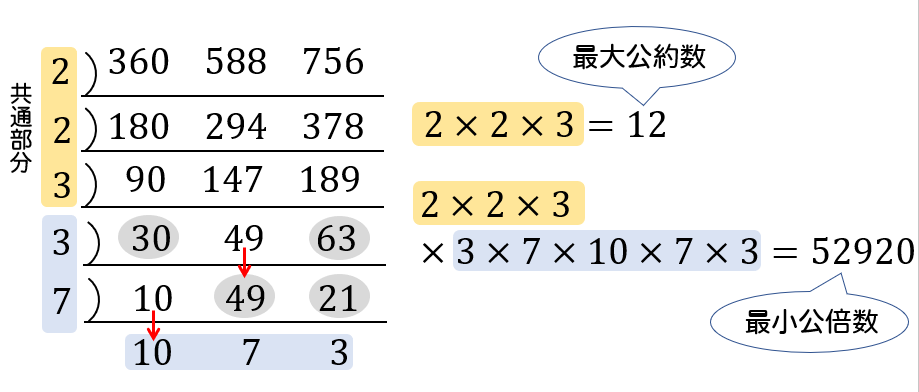



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




倍数と約数 最小公倍数 最大公約数のひみつ シリウス Edupedia




最大 公約 数 求め 方 約数と倍数の基本 最大公約数と最小公倍数の求め方まで小学生にわかる教え方 Yeah Math Stg Origin Aegpresents Com
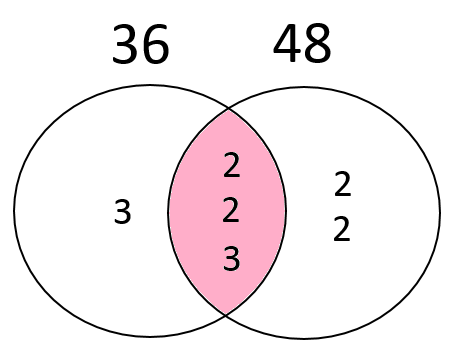



小学算数 最大公約数と最小公倍数を図を使って理解する 偏差値40プログラマー




最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場




最大公約数と最小公倍数の意味 これをタイルでイメージ出来ますか 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




最大 公約 数 求め 方 約数と倍数の基本 最大公約数と最小公倍数の求め方まで小学生にわかる教え方 Yeah Math Stg Origin Aegpresents Com
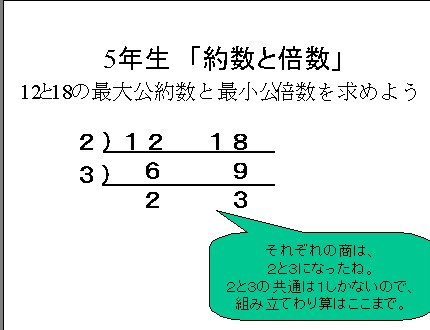



算数4年から6年
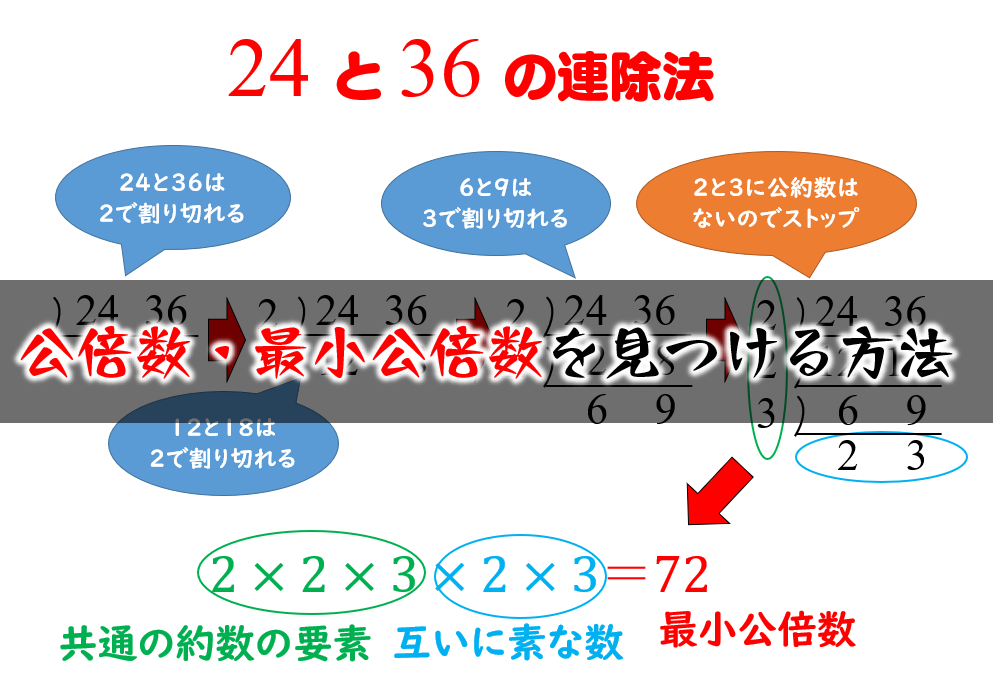



公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun



最大公約数 最小公倍数 On The App Store



2




5mx03 最小公倍数 最大公約数 親子でどんぐり




整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ
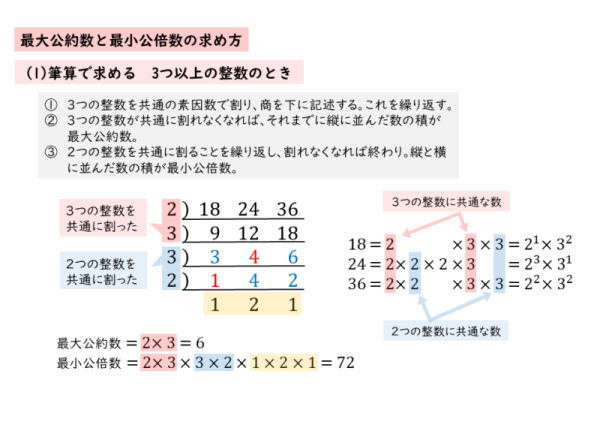



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学



整数の性質 約数と倍数 最大公約数と最小公倍数 数学学習サイト Math Kit




数学a 最大公約数と最小公倍数の関係式の使い方とコツ 教科書より詳しい高校数学




数学a整数の性質 最大公約数と最小公倍数の関係性 Youtube




最大公約数 最小公倍数の求め方 小学生算数指導にも役立ちます 塾講師ステーション情報局




最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場


