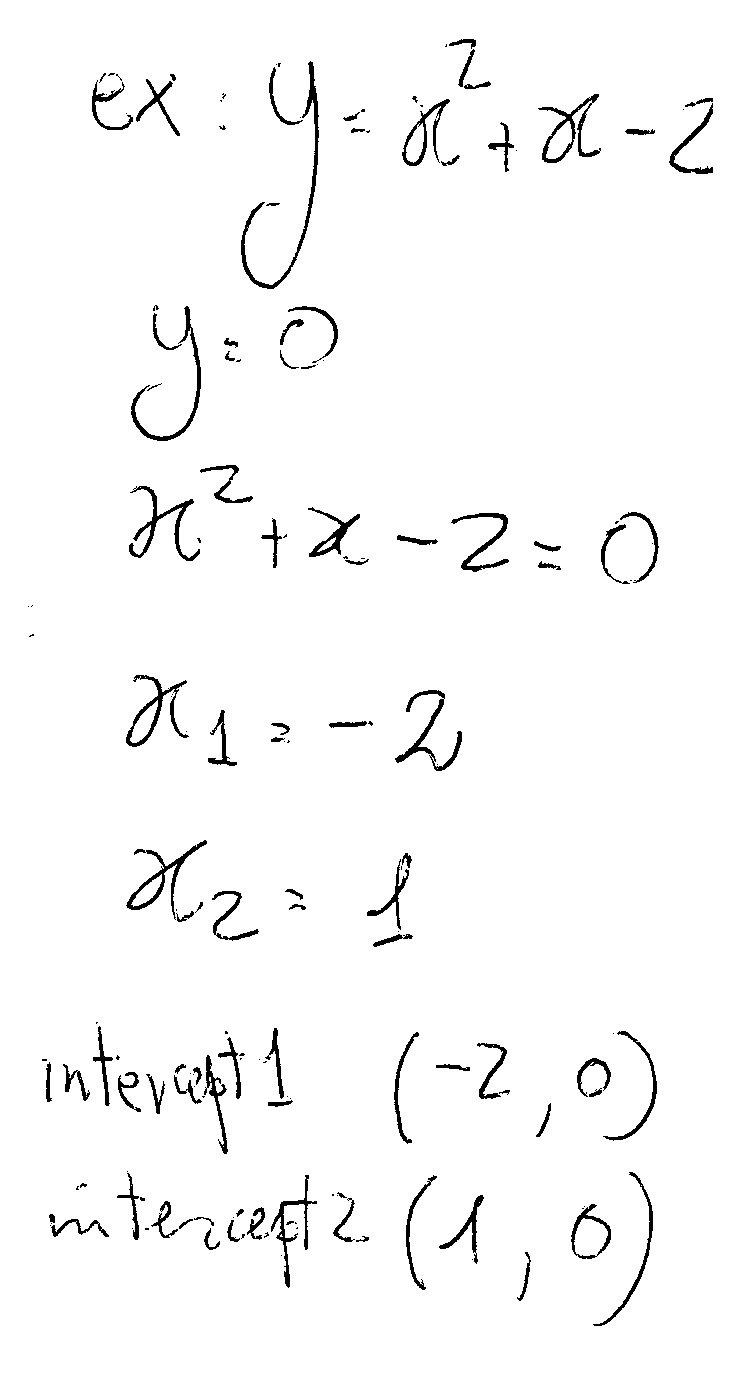結婚式で後悔したこと～披露宴～2* 飾りつけアイテムの指示書を作っておけばよかった！ 結婚式会場の飾り付けは、花嫁さん自身は行うことができません。 持ち込んだアイテムも、スタッフさんがディスプレイしてくれます＊いざ会場に行ってみると、高砂に置いて欲しかったイニシャルオブジェがなぜかウェルカムスペースになんてことは、よくあるようです12/8/21 プレ花ノート｜卒花嫁もえによるプレ花嫁のためのお悩み解決サイト 最新記事 入籍準備 指輪選び 結婚式・披露宴 結婚式・披露宴準備1/9/21 上の写真のようにテーブルクロスを使わず、お花を正面ではなくテーブルの左右に配置すれば、より身近なイメージになります。 更に 余興のない披露宴でゲスト 同士を無理に接触させる必要はありませんが、さりげなくお互いを知るためのひと工夫をしてあげることで、ゲストにより楽し リボンの他に、花や鈴などを飾りつけたり、ゲストへのメッセージを
フェスと大人可愛い装花をテーマにした笑顔の少人数披露宴 ゆきさんの挙式 披露宴ハナレポ ウエディングパーク テーブル 装花 結婚式 装飾 結婚式 テーブル 装花
動物 かわいい イラスト ライオンのイラスト素材一覧53点写真素材イラスト販売のpixtaピクスタでは4761万点以上の高品質低価格のロイヤリティフリー画像素材が660円から購入可能です 毎週更新の無料素材も配布しています 無料で使えるかわいいフリー 動物 かわいい 画像 可愛い 動物 画像 フリー 動物 の写真素材とイメージ 13,503,964 一致 ページ の 10,000 アフリカのキリン家族、野生動物、サファリ旅行の美しさ、首と戦う 2 つの動物 探して幸せで陽気な小さなヤギのかわいい動物の肖像画動物 かわいい イラスト ライオンのイラストフリー素材 犬・猫・かわいい動物や春 夏 秋 冬 季節の無料イラスト素材 ご利用規定 素材は、必ずダウンロードしてお使いください。 画像の直接呼出し（直リンク）は禁止です。 当サイト内素材の著作権は「つか」にあり放棄していません。
新品 相互評価 1アカウント1点のみ フリー画像 動物 可愛い 即決 E の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版
キミの『ポケットモンスター x・y・オメガルビー・アルファサファイア』に 色違いの「メガリザードンy （注1） 」「ピカチュウ」をプレゼント！ 当サイトに掲載しているコンテンツは攻略大百科編集部が独自に調査し作成したものです。メガフシギバナ あついしぼう プラターヌ博士からもらう ミアレシティいしやで買う メガリザードンx かたいツメ (xのみ)プラターヌ博士からもらう ミアレシティいしやで買う メガリザードンy ひでりメガリザードンx は ほのお 、 ドラゴン タイプのポケモンなので、タイプ一致のほのお、ドラゴン技を選択するのがもっともおすすめです。 中でもタイプ一致のブラストバーン は非常に強力で、ゲージも溜まりやすいため安定したダメージを与えることが可能です。
なにこれかっこいい ポケモン メガリザードンy Pixiv年鑑 B
ポケモンの人気おすすめランキング30選最高傑作を楽しもう 更新 1996年にゲームボーイ用ソフトとして登場した「ポケモン」。 1996年に初代のポケモンソフトが発売されて以降、数々の人気作品が発表されてきました。 今回は、そんなポケモンソフトの選び方やおすすめのタイトルをランキング形式で紹介します。 ポケモンホームは 過去作を持っていなかったり 有料プランにしないとポケモンを 過去作から送ってこれない等はありますが カントー御三家は無料や過去作を もっていなくてももらえる ので 是非ゲットしてみてくださいね 個人的には 夢特性 過去作との違いと新要素まとめ 2 ダイパリメイクの発売日と価格｜延期はある？ 3 バージョンごとの違いまとめ 4 御三家ポケモンのおすすめと最終進化 5 ランクマッチは存在する？
ポケモンシリーズのおすすめランキング17選 世界中で愛されている不朽の名作
Tsutaya オンラインショッピング小説・ふたりはプリキュア マックスハート/井上亜樹子 tポイントが使える・貯まるtsutaya プリキュア 小説 山田隆司 東堂いづみ 講談社キャラクター文庫 馬越嘉彦 15年9月16日に発売された『 ハートキャッチプリキュア！ 』のノベライズ版。 講談社キャラクター文庫 より『 小説 ふたりはプリキュア 』と共に発売された。 本作ではTVアニメ☆講談社キャラクター文庫の小説のご紹介です！ タイトル小説 ふたりはプリキュア マックスハート 原作東堂いづみ 著者井上亜樹子 発売日17年10月19日 ・内容・ 美墨なぎさはラクロス部の新キャプテン、雪城ほのかは科学部の新部長として、活動的な日常をすごしている。
Gri4qp Gqayf2m
Graphing Radical Functions Using Transformations You can graph a radical function of the form =y a √b (xh) k by transforming the graph of y= √ x based on the values of a, b, h, and k The effects of changing parameters in radical functions are the same asSection 12 Transformations of Linear and Absolute Value Functions 13 Writing Refl ections of Functions Let f(x) = ∣ x 3 ∣ 1 a Write a function g whose graph is a refl ection in the xaxis of the graph of f b Write a function h whose graph is a refl ection in the yaxis of the graph of f SOLUTION a A refl ection in the xaxis changes the sign of each output valueK is the vertical translation if k is positive, shifts up if k is negative, shifts down k also shifts the horizontal asymptote a is orientation and shape if a is negative, reflection across xaxis if a > 1, stretched vertically if 0 < a < 1, compressed vertically Example Graph, then state the domain, range and asymptotes \(f(x) = \frac{2}{{x
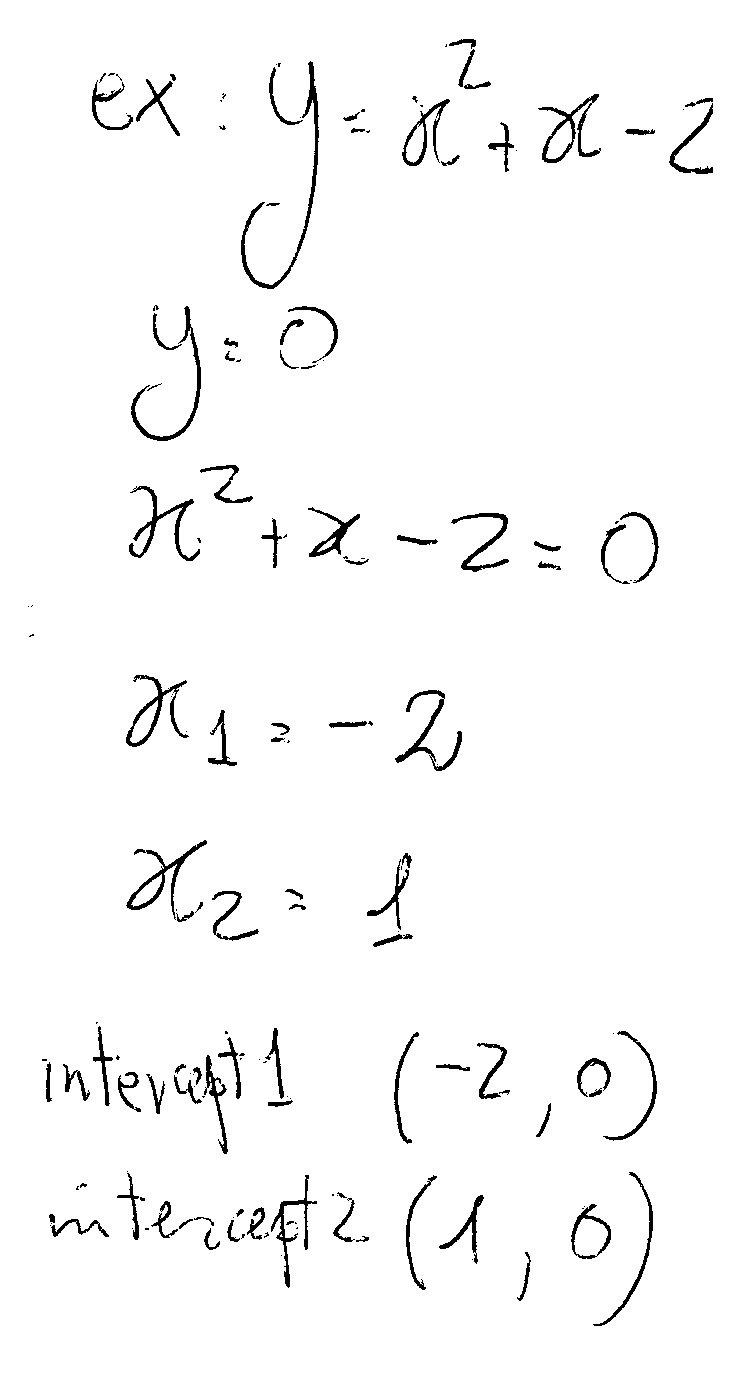
Quadratic Functions And Their Graphs Algebra Socratic
プリキュア キックボード ＞ 今日お届け★代引・送料無料★ちゃりんくるスクーター スイートプリキュア11年モデル m&m エムアンドエム キックボード スクータートイザらス限定 EVO キックスクーター ピンク AVIGO;プリキュア キックボードの情報 「プリキュア キックボード」は1件の商品が出品がされています。 「プリキュア キックボード」と関連する商品には 、魔改造フィギュア 、靴下 、前売 、半袖 、スポーツタオル などがあります。
全ての 新品 Go プリンセスプリキュア ちゃりんくるスクータ ー 国産 Www Eatforhealth Gr
